Inflazione, tassi di interesse nominali, tassi reali e mutui a tasso variabile

Ciò che conta per l’economia e anche per la distribuzione del reddito fra creditori e debitori non sono i tassi di interesse nominali, ma i tassi di interesse reali, ossia i tassi nominali al netto dell’inflazione. Sono questi, infatti, che tipicamente entrano nella determinazione delle variabili chiave dei modelli econometrici. La confusione fra tassi nominali e tassi reali è all’origine di polemiche non sempre correttamente argomentate contro le banche centrali, per via dei recenti aumenti dei tassi di policy, e contro il sistema bancario, in relazione in particolare alla questione dei mutui a tasso variabile. Nel seguito, cerchiamo di fare un po’ di chiarezza sui concetti e su come essi debbano essere applicati ai casi concreti. Si può criticare la BCE (così come la Fed) per tante ragioni, ma, se si tiene conto dell’inflazione, è difficile dire che oggi i tassi di interesse siano troppo alti. Nei mutui a tasso variabile, al crescere dell’inflazione e dunque dei tassi nominali non si verifica una redistribuzione della ricchezza a favore della banca, se il tasso di interesse reale viene mantenuto costante. Tuttavia, anche in questo caso, la rata aumenta più dell’inflazione; questa circostanza non dipende dal comportamento delle banche, ma ai mutuatari può creare problemi gravi di cui la Banca d’Italia e l’Associazione Bancaria Italiana sono ben consapevoli, tanto che hanno cercato di porre qualche rimedio. Il mutuo a tasso variabile è una scelta rischiosa che dovrebbe essere seriamente sconsigliata a una normale famiglia in cerca di un finanziamento per l’acquisto della prima casa.

* * *

Forse per via del lungo periodo di inflazione bassa o nulla che ha interessato quasi tutti i Paesi avanzati dopo gli anni Ottanta, sembra che si sia quasi persa la memoria della fondamentale differenza fra tassi di interesse nominali e tassi di interesse reali e del fatto che ciò che conta per l’economia e anche per la distribuzione del reddito fra creditori e debitori non sono i tassi di interesse nominali, bensì i tassi di interesse reali, ossia i tassi nominali al netto dell’inflazione. In una semplice formula:

r ≅ i - infl

Il tasso di interesse reale (r) è quasi uguale (≅) al tasso di interesse nominale (i) meno il tasso di inflazione (infl).^[1] In ogni caso, vi deve essere coerenza fra il tasso di interesse e l’inflazione. Per esempio, se l’interesse è quello dei BOT a 6 mesi dell’anno scorso, bisogna che l’inflazione sia quella verificatasi nei sei mesi corrispondenti dell’anno scorso. Le cose sono molto più complicate quando si considerano i tassi di interesse su un orizzonte futuro: per esempio, il tasso di interesse su un BOT a 12 mesi oggi deve essere paragonato con l’inflazione che ci si attende oggi per i prossimi 12 mesi. Questo richiede di rispondere a molte domande (su cui sorvoliamo in questa nota) su quali siano gli operatori rilevanti (il generico consumatore può avere aspettative diverse da un operatore finanziario), su come si misurino e come si formino le aspettative.

La confusione fra tassi nominali e tassi reali è all’origine di polemiche non sempre correttamente argomentate contro le banche centrali, per via dei recenti aumenti dei tassi di policy, e contro il sistema bancario, in relazione in particolare alla questione dei mutui a tasso variabile. Nel seguito, cerchiamo di fare un po’ di chiarezza su questi concetti e su come essi debbano essere applicati ai casi concreti.

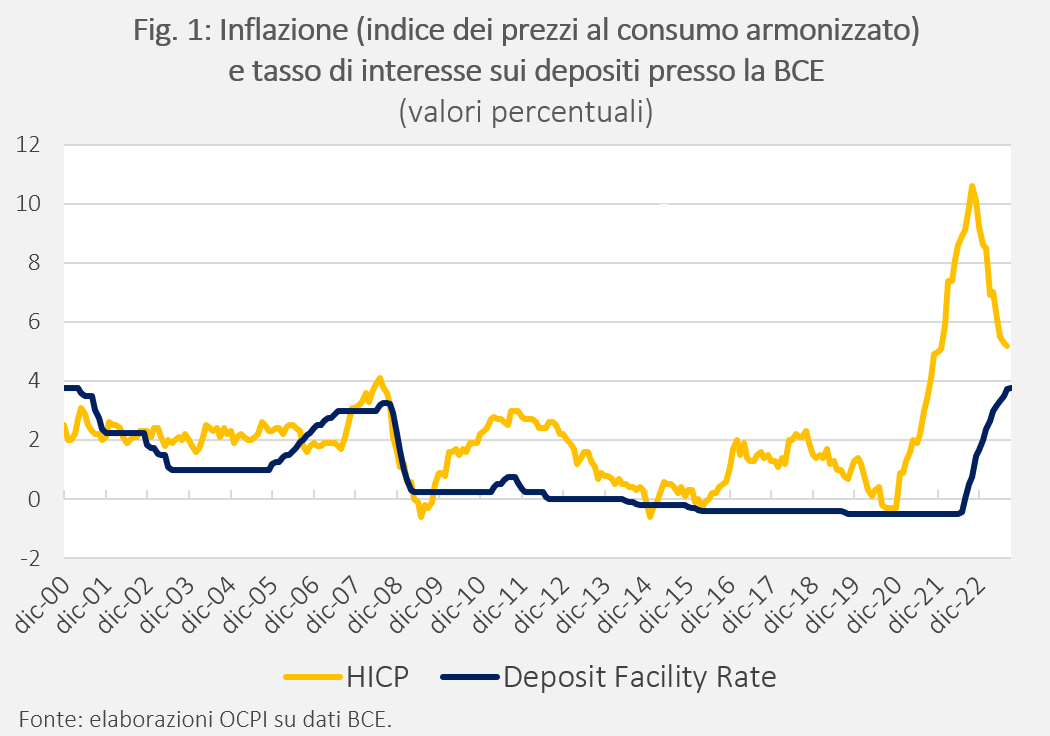
Preliminarmente però è utile ricordare che il principale tasso di policy della BCE, quello sui depositi delle banche presso la banca centrale, è oggi al 4 per cento. L’inflazione ad agosto 2023 era al 5,2 per cento. Quindi anche solo sottraendo i due termini si ha che il tasso di intessere reale è negativo. Come si vede dalla Fig. 1, il tasso di interesse sui depositi presso la BCE si è impennato dal luglio dell’anno scorso ed è salito da un valore negativo (-0,5 per cento) fino al 4 per cento dal 20 settembre scorso. L’aumento è stato però di gran lunga inferiore all’aumento dell’inflazione che è passata da -0,3 per cento nel dicembre 2020 fino a un picco di 10,6 per cento a ottobre del 2022. Il che significa che negli ultimi tre anni il tasso di interesse reale (della BCE) è stato negativo in una misura che non ha precedenti nella storia dell’Unione Monetaria. Si può certamente criticare la BCE per tanti motivi: per esempio, molti economisti la criticano per avere reagito in ritardo e in modo troppo brusco rispetto all’aumento dell’inflazione e ritengono che questo modo di operare crei dei rischi perché non consente agli operatori di adattarsi gradualmente al nuovo contesto economico. Ma è difficile criticare la BCE (così come la Fed) perché i tassi di interesse sono oggi troppo alti. Rispetto all’inflazione, ossia in termini reali, non sono affatto alti.

Chi ci guadagna e chi ci perde?

La considerazione fondamentale che si può fare riguardo a situazioni in cui il tasso di interesse reale è negativo è che ci guadagnano i debitori e ci perdono i creditori. Fra i debitori c’è innanzitutto lo Stato, ma ci sono anche le famiglie e le imprese che sono indebitate con le banche o con i mercati. Naturalmente, per calare quest’affermazione nei casi concreti occorre considerare i tassi di interesse che pagano effettivamente gli Stati, le imprese e le famiglie. È necessario anche chiedersi se i redditi dei diversi operatori tengano il passo con l’inflazione; una famiglia che si vede aumentare la rata di un mutuo a tasso variabile ha una perdita evidente se le sue entrate non sono aumentate come l’inflazione. Nell’aggregato, tuttavia, a meno della tassa che si paga all’estero per il rincaro delle materie prime importate, l’insieme dei debitori ci guadagna rispetto all’insieme dei creditori.

Queste affermazioni hanno implicazioni che vanno ben oltre la mera percezione dell’opinione pubblica, un fatto comunque importante per i risvolti che ha in termini di consenso politico. La confusione fra tassi di interesse nominali e reali può riguardare anche i mercati finanziari e avere effetti reali sui valori di borsa. In un famoso articolo del 1979, Franco Modigliani e Richard Cohn argomentarono che il declino della borsa USA dalla fine degli anni Sessanta era dovuto all’inflazione e al fatto che gli investitori non coglievano appieno il fatto che il valore reale dei debiti delle imprese si stesse svalutando con l’inflazione; vedevano crescere gli oneri finanziari delle imprese, ma non vedevano che tali oneri erano solo la contropartita di crediti svalutati.^[2]

La questione non è dunque banale e merita una piccola dimostrazione tramite qualche semplice esempio.

Qualche semplice calcolo

L’affermazione di fondo è che bisogna guardare ai tassi di interesse reali per capire chi guadagna e chi perde fra creditori e debitori in un contesto inflazionistico. 

Consideriamo il caso di un debito di 1.000 euro e di tassi di interesse reali pari all’1 per cento. Nella Tav. 1, nella prima colonna si considera il caso di un’inflazione pari a zero. In questo caso, il tasso di interesse nominale è uguale al tasso di interesse reale (1 per cento). A fine anno (se si suppone che il debito abbia scadenza un anno) il debitore deve euro 1.000 x (1+1%) = 1.010.

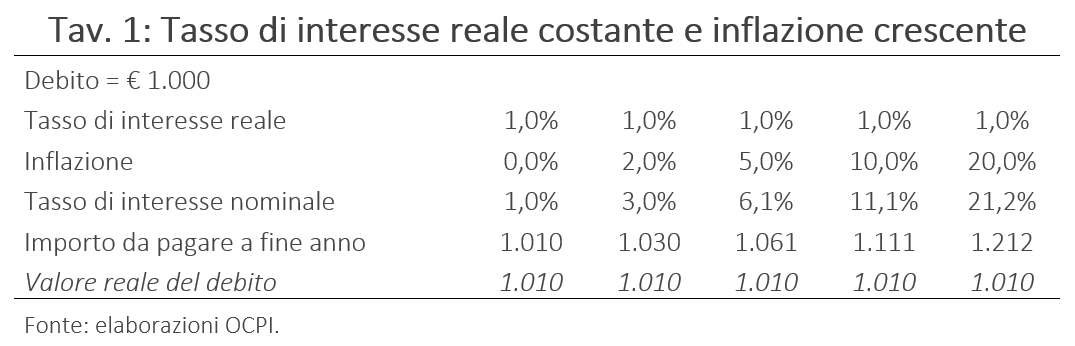
Ora, tenendo fermo il tasso di interesse reale si considerano diversi tassi di inflazione (dal 3 al 20 per cento). Ovviamente, dato che il tasso nominale cresce con l’inflazione la somma da pagare a fine anno cresce al crescere dell’inflazione e nel caso di inflazione al 20 per cento arriva a 1.212. Nella contabilità di un’azienda il valore della passività rimane 1.000 e gli oneri finanziari salgono a 212. Queste cifre sono quelle su cui tipicamente si sofferma l’attenzione del debitore e anche di tanta parte dell’opinione pubblica. In realtà ciò a cui si dovrebbe guardare è l’ultima riga della tabella che mostra il valore reale del debito in euro di oggi. Se nel corso di un anno l’inflazione è stata del 20 per cento, il valore reale, ossia in euro di oggi, del debito dovuto domani rimane uguale a 1.010. Il punto è che il maggior tasso nominale rispetto al caso di inflazione zero (o comunque più bassa) non fa altro che compensare il creditore per la svalutazione del suo credito dovuta all’inflazione. Infatti, un credito di 1.212 euro domani vale esattamente 1.010 in euro di oggi.^[3]

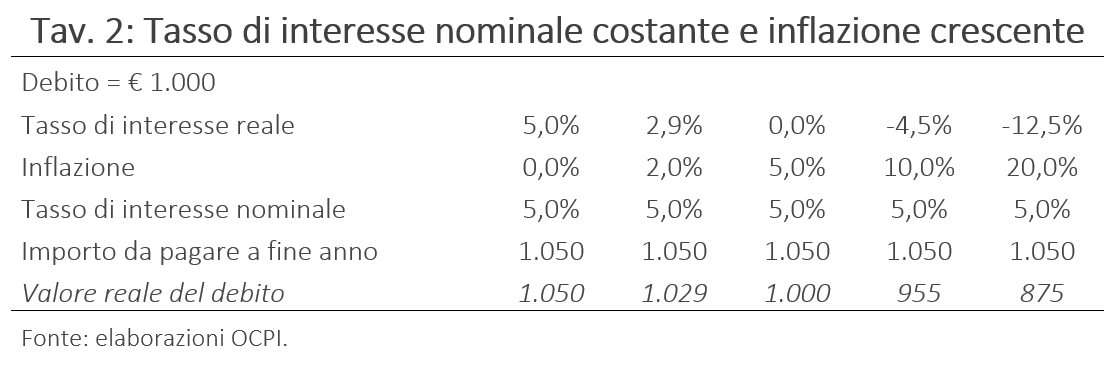
Nella Tav. 2 consideriamo il caso di un tasso nominale fisso (al 5 per cento annuo) e, come prima, un’inflazione crescente. Quando l’inflazione è zero, il tasso reale (calcolato a saldo) è uguale al tasso nominale (5 per cento). Man mano che sale l’inflazione, il tasso reale scende, fino a raggiungere lo zero, quando l’inflazione è proprio 5 per cento; per valori più alti dell’inflazione assume valori negativi.^[4] In questo caso il debitore deve sempre la stessa cifra (1.050) indipendentemente dall’inflazione. Tuttavia, il valore reale di 1.050 euro è molto diverso a seconda dell’inflazione. Con inflazione zero il valore rimane 1.050, ma con inflazione al 20 per cento il valore scende a 875. Il che significa in pratica che il creditore presta dei soldi e ha un ritorno negativo. Questo non è un evento raro: in effetti, chi oggi investe in titoli di Stato a breve termine – di qualunque Paese avanzato – sa che a scadenza otterrà un capitale il cui valore reale è inferiore al capitale investito.

Vedendo le cose dal punto di vista dello Stato, la svalutazione del debito è un grande vantaggio ed è infatti il motivo principale per il quale il rapporto fra debito pubblico e Pil è diminuito dal 2021 a oggi.

I rischi dei mutui a tasso variabile

L’affermazione centrale di questa nota (che contano i tassi di interesse reali) necessita di qualche qualificazione, la principale delle quali riguarda il fatto che la duration di un titolo di debito (non indicizzato all’inflazione) dipende dai tassi di interesse nominali e non da quelli reali. La duration può essere tradotta come durata finanziaria del titolo di debito ed è calcolata come la media ponderata delle scadenze in cui verranno versate le cedole e il rimborso del capitale. Quando aumentano le cedole (perché il tasso nominale aumenta) la duration diminuisce, il che significa che una quota maggiore del debito viene pagata anticipatamente. Solo nel caso di titoli a cedola zero (per esempio un BOT a 12 mesi), la duration coincide con la scadenza (12 mesi). In tutti i casi in cui vi è un pagamento periodico di cedole o quote di capitale, la duration diminuisce quando aumentano i tassi nominali. Questa caratteristica dei titoli di debito ha un importante corollario nel caso dei mutui ipotecari.

In teoria, la situazione di una famiglia che abbia un debito con la banca, per esempio un mutuo ipotecario, non è diversa da quella dello stato che guadagna dall’inflazione: se il tasso sul mutuo (sia esso a tasso fisso o variabile) è inferiore all’inflazione vi un trasferimento di ricchezza dalla banca alla famiglia.

In pratica, a un’inflazione più alta corrispondono rate di mutuo più elevate in termini reali nei primi periodi della vita del mutuo e questo può creare problemi a chi deve comprare casa. Il problema si complica ulteriormente nel caso di mutui a tasso variabile. Ma andiamo con ordine e consideriamo prima i mutui a tasso fisso.

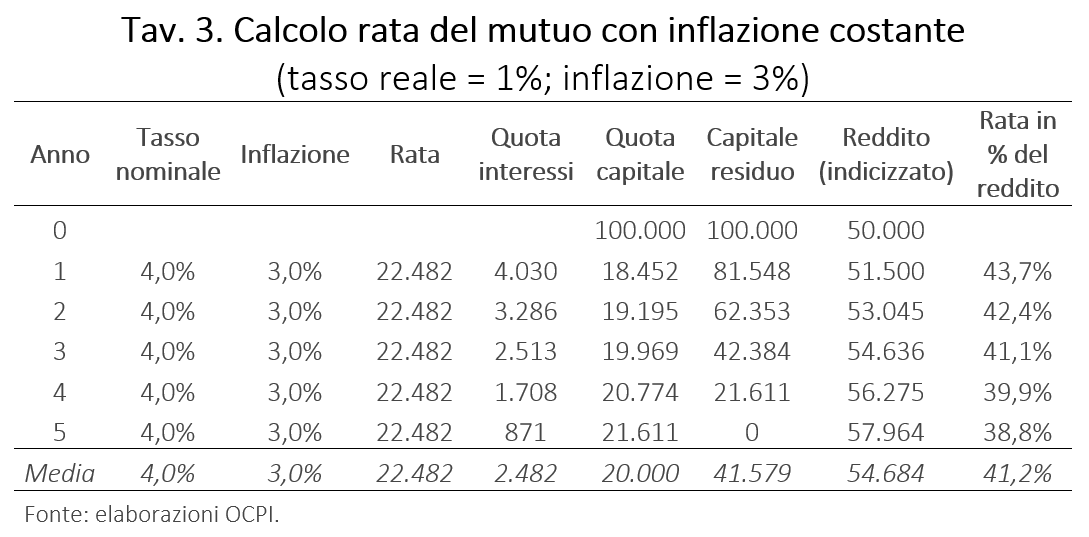
Per chiarire il punto si consideri la Tav. 3 in cui si calcola la rata di un mutuo quinquennale a tasso fisso con rata annuale,^[5] con inflazione costante (3 per cento l’anno) e tasso reale al 1 per cento.^[6] Se si ipotizza che il reddito del mutuatario (50.000 euro inizialmente) cresca come l’inflazione, la rata del mutuo (costante se valutata a prezzi correnti), diminuisce in percentuale del reddito, dal 43,7 per cento al 38,8 per cento.^[7] In media il rapporto fra la rata e il reddito si attesta a 41,2 per cento (ultima riga dell’ultima colonna).

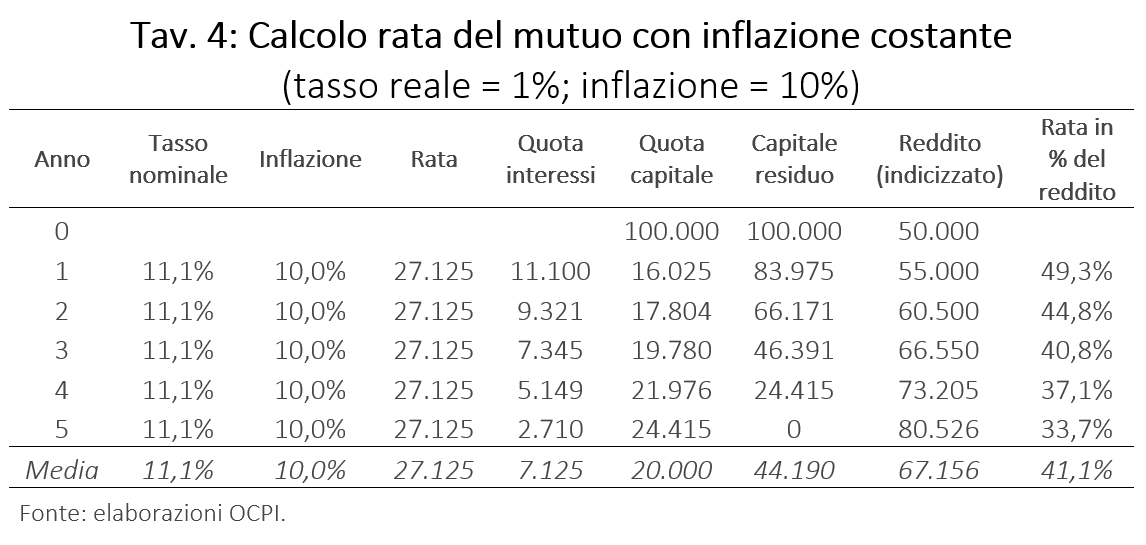
Nella Tav. 4 si considera un mutuo identico al precedente (scadenza a cinque anni; rata annuale; tasso reale all’1 per cento) con l’unica differenza che ora l’inflazione è del 10 per cento^[8]. Come si vede, in media, lungo l’intera vita del mutuo, la rata rimane attorno al 42 per cento del reddito, il che è un semplice corollario del punto centrale di questa nota: ciò che conta è il tasso reale. La differenza è che nei primi anni la rata è molto più pesante in rapporto al reddito. Nel primo anno è al 49,3 per cento del reddito, mentre nell’altro caso (con inflazione al 3 per cento), la rata era al 43,7 per cento. Alla fine della vita del mutuo, il peso della rata è minore nel caso in cui l’inflazione è più alta. Aritmeticamente, la ragione per cui con inflazione più alta la rata è più pesante all’inizio è che la quota interessi è più alta perché in questo caso si ha l’11,1 per cento di 100.000 e nell’altro il 4 per cento di 100.000.

La rata elevata nei periodi iniziali della vita del mutuo può rendere difficile l’accesso la mutuo, soprattutto per persone giovani, che in genere all’inizio del percorso lavorativo hanno redditi bassi. Il problema si aggrava ovviamente se non è realizzata l’ipotesi di un aumento del reddito in linea con l’inflazione. Se il reddito rimane costante a 50.000, il peso della rata rimane al 49,3 per cento per tutta la durata del mutuo.

Il problema si ripropone, in termini più problematici, nel caso dei mutui a tasso variabile. Nella Tav. 5 si considera un mutuo a tasso variabile che ha in comune con i precedenti il fatto di avere un tasso di interesse reale costante e uguale a 1 per cento^[9]. L’inflazione rimane al 3 per cento nel primo anno e poi balza al 10 per cento. Come ovvio, la rata sale moltissimo perché il tasso nominale è passato da 4,0 a 11,1 per cento. Come prima, nell’ultima colonna è calcolato il rapporto fra la rata e il reddito del mutuatario, che anche in questo caso si assume cresca con l’inflazione. Come si vede, il rapporto fra la rata e il reddito è in media 41,2 per cento, circa lo stesso valore dei precedenti esercizi. Ancora una volta, ciò che conta è il tasso di interesse reale.

E tuttavia ci sono due problemi. Il primo, già menzionato, è che spesso ci vuole tempo prima che i redditi (da lavoro dipendente) recuperino il potere d’acquisto perso con l’inflazione. Per questo solo motivo, a volte i mutui a tasso variabile diventano insostenibili.

Il secondo problema è che nel momento in cui l’inflazione aumenta, la rata del mutuo aumenta più dell’inflazione. Come si vede nella colonna “Rata” della tabella, nel secondo anno la rata aumenta da 22.482 euro a 26.341, che corrisponde a +17 per cento. L’inflazione è invece aumentata al 10 per cento.

Il fatto che la rata aumenti più dell’inflazione è un problema reale ed è oggetto di sconcerto dell’opinione pubblica e di proteste da parte delle associazioni dei consumatori. Il pensiero comune, di chiunque non abbia una specifica competenza in economia o finanza, è che la rata dovrebbe comportarsi come un qualunque bene di consumo e aumentare tuttalpiù come aumentano i prezzi. Si aggiunga che, quando si considerano mutui a più lungo termine, l’aumento della rata in corrispondenza di aumenti dei tassi nominali è molto più marcata e può anche aumentare del 30 o 50 per cento. Ed è difficile spiegare che l’aumento è coerente con quanto pattuito nel contratto di mutuo e che nel corso del tempo, il problema svanisce: infatti, nel nostro esempio, alla fine della vita del mutuo, la rata scende al 34,9 per cento del reddito a fronte del 38,8 per cento del corrispondente mutuo a tasso fisso (quello della Tav. 3 con inflazione inziale al 3 per cento). Il motivo per il quale la rata aumenta più dell’inflazione è la stessa del caso precedente. La quota interessi della rata sale in proporzione al tasso di interesse nominale. Il problema è particolarmente acuto quando si verifica nei primi anni di vita di un mutuo a tasso variabile, perché nei primi anni la quota interessi ha un peso preponderante sulla rata.

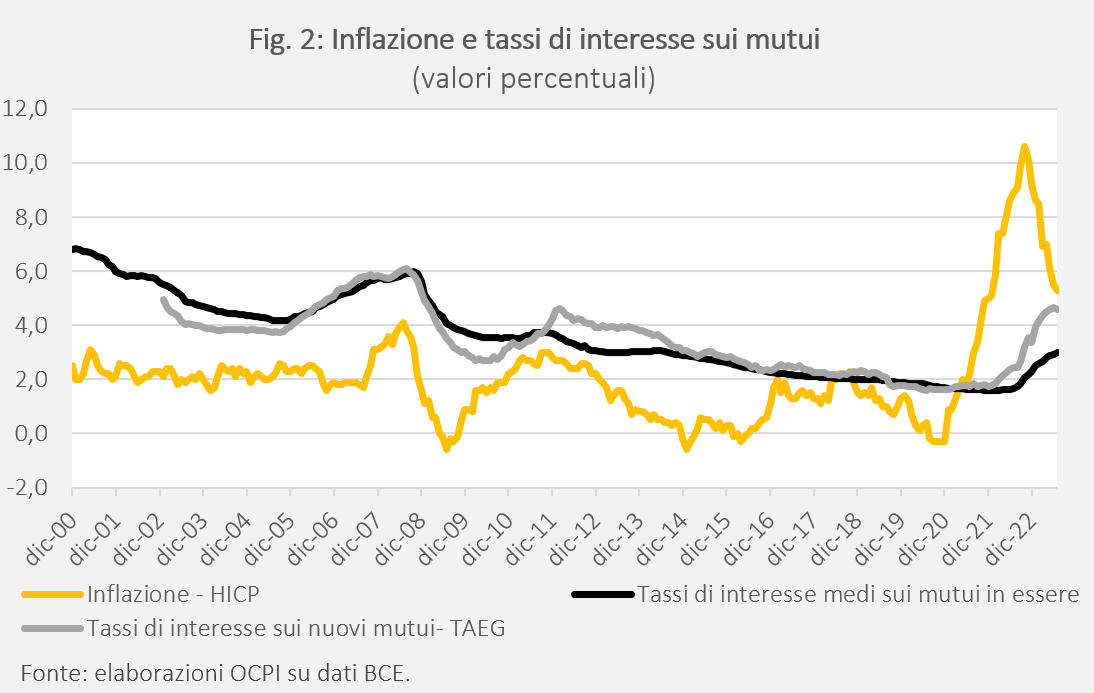
Non vi è dunque nulla da recriminare nei confronti dei banchieri. Tanto più in un periodo come l’attuale in cui i tassi interesse medi (a tasso fisso e variabile) sui mutui sono inferiori all’inflazione sia sui nuovi mutui sia, a maggior ragione, sul totale dei mutui in essere (Fig. 2).

E tuttavia il problema esiste, tant’è che di recente l’ABI (Associazione Bancaria Italiana) ha diramato una circolare in cui propone alle proprie associate una serie di soluzioni, quali l’allungamento del piano di ammortamento, il ricorso al Fondo di Solidarietà per i mutui prima casa che consente di sospendere – al verificarsi di specifici eventi – il pagamento delle rate, l’allargamento a una platea più ampia di quella prevista per legge della possibilità di rinegoziare il mutuo.^[10]

Appendice: i tassi di interesse nei modelli econometrici

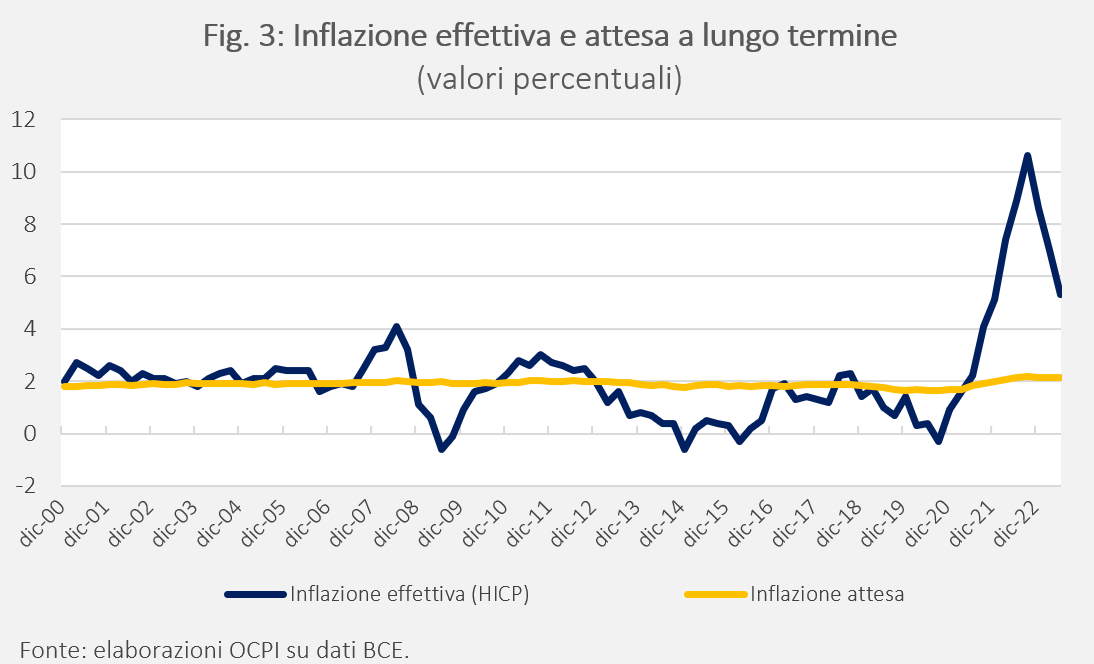
In quasi tutti i modelli econometrici il tasso di interesse che rileva nelle equazioni dell’economia reale (consumi, investimenti, rapporto desirato fra capitale e lavoro ecc.) è il tasso di interesse reale. Ciò è sicuramente vero in tutti i modelli delle banche centrali di cui si è trovata evidenza.^[11] Di solito si assume che ciò che rileva sia il tasso di interesse reale e raramente questa ipotesi è sottoposta a test statistici, probabilmente in quanto la si ritiene ovvia. Va però detto che un ruolo per i tassi nominali può riapparire se si tiene conto del fatto che l’inflazione che serve alla definizione dei tassi di interesse reali è di solito l’inflazione attesa. Per esempio, l’investimento in macchinari tipicamente dipende da un tasso di interesse a lungo termine (definito in funzione delle fonti di finanziamento dell’impresa) il quale va ovviamente confrontato con l’inflazione attesa sullo stesso periodo di tempo. Dunque, se il tasso di interesse riguarda uno strumento di debito con scadenza decennale, l’inflazione attesa deve anch’essa essere l’inflazione a 10 anni. In genere i modelli usano i risultati delle survey fra gli operatori (imprese, consumatori, operatori finanziari a seconda dei casi) e cercano di modellare queste aspettative con delle equazioni di tipo autoregressivo (ARIMA). In base ai risultati delle stime, a variazioni del tasso di inflazione effettivo in un dato periodo (per esempio, un trimestre, se il modello è trimestrale), possono corrispondere variazioni più o meno proporzionali del tasso di inflazione atteso. Di solito, le aspettative a lungo termine reagiscono lentamente a variazioni dell’inflazione effettiva. In questo caso, può apparire che il tasso di interesse rilevante sia quello nominale, proprio perché le aspettative si muovono poco. In questo caso però l’affermazione più corretta è che il tasso che conta è il tasso di interesse reale percepito dagli operatori. E naturalmente è ben possibile che un generico consumatore si renda conto con maggiore ritardo di un’impresa o di un operatore finanziario delle variazioni dell’inflazione e degli effetti che questa ha sul tenore di vita e su tutte le altre variabili rilevanti (consumi durevoli e non, risparmio ecc.). Un ruolo importante ha in alcuni modelli (per esempio in quello della BCE), il tasso di inflazione obiettivo della banca centrale: se la banca centrale è credibile le aspettative a medio lungo termine rimangono “ancorate” all’obiettivo (2 per cento nel caso della BCE e della Fed). Se questo è vero, al variare dell’inflazione effettiva le aspettative a medio-lungo termine (che sono quelle, per esempio, determinanti per le scelte di investimenti) si dovrebbero muovere molto poco al variare dell’inflazione effettiva. La Fig. 3 mostra che negli ultimi anni l’inflazione effettiva è aumentata molto, ma le aspettative di inflazione a lungo termine sono rimaste molto vicine all’obiettivo del 2 per cento. 

Nel modello della BCE, l’inflazione attesa a lungo termine si adegua lentamente a una media ponderata del tasso obiettivo della BCE (con coefficiente uguale a 0,4) e del tasso di inflazione effettivo (con coefficiente 0,6). L’adeguamento è piuttosto lento in quanto le aspettative del periodo precedente hanno un coefficiente elevato (0,75).^[12] Sia un aggiustamento lento sia un basso valore del coefficiente dell’inflazione obiettivo possono segnalare scarsa credibilità della banca centrale. Va però detto che l’ultima versione disponibile del modello è stato pubblicato nel settembre del 2019 e dunque prima che la credibilità della BCE fosse soggetta al test dell’alta inflazione degli ultimi tre anni.

La mancata considerazione del ruolo della credibilità della banca centrale e del suo obiettivo potrebbe il motivo per il quale in alcuni modelli (per esempio in quello di Ray Fair, un econometrico dell’università di Yale molto stimato e sicuramente accurato) si trovano effetti separati dei tassi nominali e dei tassi di inflazione^[13]. E può anche essere uno dei motivi per i quali molto spesso per gran parte dell’opinione pubblica contano di più i tassi di interesse nominali di quelli reali.