Perché il COVID-19 ha colpito i paesi in modo diverso?

Perché il COVID-19 ha colpito i paesi in modo diverso?

di Carlo Cottarelli e Federica Paudice

11 marzo 2021

Esistono marcate differenze tra paesi nel numero di decessi causati dal Covid-19. Perché? Questa nota passa in rassegna i lavori fin qui prodotti per rispondere a questa domanda e fornisce ulteriore evidenza empirica sull’argomento considerando, per la prima volta, il totale dei decessi registrato nel 2020. Il complesso dell’evidenza disponibile porta a concludere che la struttura demografica della popolazione, l’ordine in cui sono stati colpiti i vari paesi (i paesi colpiti prima sono stati penalizzati), l’inquinamento atmosferico sono stati fattori particolarmente rilevanti. Non sembra invece che il livello della spesa pubblica per la sanità nel periodo pre-Covid sia stato rilevante, forse perché paesi ad alta spesa non erano comunque preparati alla sorpresa di una pandemia. Resta comunque appropriato un aumento della spesa sanitaria pubblica nel nostro paese, visto il basso livello raggiunto nel corso dell’ultimo decennio.

La nota è stata ripresa da Repubblica in questo articolo del 13 marzo 2021

* * *

Il virus ha colpito diversi paesi in modo differente. Anche guardando soltanto a un gruppo di paesi relativamente omogeneo, come i paesi cosiddetti “avanzati”, le differenze nel 2020 nel numero dei decessi sono enormi. Si passa dai valori minimi di Nuova Zelanda e Corea del Sud (rispettivamente 1 e 2 decessi ogni 100.000 abitanti) al valore massimo del Belgio (171 decessi; Fig.1). Cosa spiega queste differenze? Diversi lavori hanno cercato di spiegare i diversi sviluppi del contagio tra paesi. Passiamo in rassegna questi lavori nella sezione 1, anche come base per presentare ulteriore evidenza empirica nelle seguenti sezioni di questa nota.

 

Rassegna della letteratura

Una vasta letteratura cerca di spiegare quali variabili hanno determinato il diverso grado di severità della pandemia Covid tra aree geografiche nel 2020. Di seguito viene presentata una rassegna di 16 studi che indagano questo aspetto attraverso l’uso di modelli statistici.^[1] Le variabili dipendenti utilizzate all’interno dei modelli sono: il tasso di fatalità (rapporto tra i decessi e i contagi), il tasso di mortalità (rapporto tra decessi e popolazione) e il numero o il tasso di contagiati (rapporto tra contagiati e popolazione).^[2]

Le variabili indipendenti incluse per spiegare le differenze possono essere ricondotte a 5 tipologie: demografiche e relative allo stato di salute della popolazione, socioeconomiche, ambientali, variabili relative alle misure adottate e alla risposta da parte dei cittadini e variabili relative alla capacità dei sistemi sanitari.

• Variabili demografiche e relative allo stato di salute della popolazione

La maggior parte degli studi trova una relazione tra anzianità della popolazione e severità del virus. Vi sono evidenze del nesso tra fatalità e presenza di patologie cardiovascolari/respiratorie e di cancro, mentre i risultati sono contrastanti circa il ruolo di altri fattori di rischio (quali obesità e fumo).

Tutti i modelli descritti nella rassegna, eccetto 4 (Austin et al., Cartenì et al., Olivieri et al. e Zhu et al.), tengono conto dell’età della popolazione. Solo in 2 casi, si riscontra sorprendentemente che l’anzianità della popolazione non è un fattore significativo nello spiegare la differente mortalità del virus tra aree (Chaudry et al. e Knittel et al.), benché sia evidente che le fasce più anziane di popolazione sono state le più colpite. Solitamente gli studi, per tenere conto dell’età della popolazione, utilizzano variabili come la percentuale di popolazione con età superiore ad una soglia (solitamente 65, 70 o 80 anni), oppure l’età mediana. Ingo et al., invece, al fine di tenere conto della maggiore vulnerabilità della popolazione anziana, conducono analisi separate sulla popolazione divisa per fasce di età e, concentrandosi sulle regioni tedesche, trovano che piccole variazioni delle variabili indipendenti (con particolare riferimento all’inquinamento) possono comportare significative variazioni della mortalità tra le fasce più anziane. Anche il recente rapporto dell’Istituto Sanitario di Sanità (ISS, 2021) pubblicato il 20 gennaio 2021 che si concentra su un confronto tra i tassi di fatalità tra regioni italiane, considera i tassi di fatalità standardizzati per l’età al fine di tenere conto del brusco aumento del tasso per gli over 50. Il ricorso al metodo della standardizzazione consente così di evitare distorsioni nei confronti tra regioni italiane dovute alle diverse distribuzioni nei decessi per età.^[3]

Con l’intento di cogliere lo stato di salute della popolazione, vengono spesso incluse variabili relative alla presenza di patologie sul territorio e fattori di rischio (ad esempio la percentuale di fumatori e obesi). Sorci et al., analizzando un campione di 143 paesi, concludono che la presenza di malattie cardiovascolari, respiratorie e cancro aumenta il grado di fatalità del virus.^[4] Vi sono invece risultati discordanti circa il ruolo di altri fattori di rischio per la salute: Sorci et al. trovano una relazione positiva tra tasso di fatalità e percentuale di fumatori tra gli over 70, Chaudhry et al., concentrandosi su un campione di 50 paesi, concludono che l’obesità e il fumo sono correlati sia alla mortalità, sia ai casi, mentre Knittel et al. e Wu et al. non trovano alcuna relazione tra mortalità negli Stati Uniti e fattori di rischio quali obesità e fumo.

• Variabili socioeconomiche

Sorprendentemente, nei confronti tra paesi, il reddito e il Pil pro-capite sembrano essere positivamente correlati al grado di severità della pandemia. Tuttavia, la relazione scompare se si studiano le differenze tra aree all’interno dello stesso paese.

Nonostante le incertezze sulla misurazione del fenomeno, il Covid sembra aver colpito più duramente i paesi avanzati, con perdite umane minori per aree a reddito basso, come l’Africa. I lavori statistici considerati trovano in effetti una ricorrente correlazione positiva tra il livello di reddito e il grado di severità della pandemia tra paesi (tra questi Sorci et al., Chaudry et al. e Wu et al.). Questa correlazione, per lavori che non controllano adeguatamente per la struttura demografica della popolazione, potrebbe riflettere la minore età media dei paesi a reddito basso. Potrebbe anche essere dovuta al migliore tracciamento e alla maggiore trasparenza dei dati provenienti dai paesi ad alto reddito. Infatti, gli studi che guardano all’interno dei singoli paesi trovano una relazione non significativa con la mortalità sia con segno negativo (Cole et al., che analizzano i comuni olandesi), sia con segno positivo (Becchetti et al., che analizzano le province del Nord Italia).

Con riferimento all’etnia della popolazione, sia Wu et al., sia Knittel et al. riscontrano una relazione positiva tra mortalità e presenza di afroamericani negli Stati Uniti, probabilmente legata al maggiore disagio sociale e lavorativo di queste fasce di popolazione, relativamente più colpiti dal Covid. È questa anche la tesi di Cole et al. che riscontrano una relazione positiva e significativa tra immigrati non occidentali e tasso di mortalità nelle diverse provincie dei Paesi Bassi. Coker et al. e Becchetti et al., invece, concentrandosi sul Nord Italia, non riscontrano alcuna correlazione rispettivamente tra mortalità e presenza di immigrati non europei e diffusione del contagio e presenza di immigrati cinesi.

• Variabili ambientali

L’insieme degli studi presi in esame prova che il legame tra inquinamento e severità della pandemia esiste ed è robusto.

L’indicatore di inquinamento più utilizzato è la concentrazione di particelle PM (o particolato o polveri sottili, spesso nella forma di PM2.5, quelle di dimensioni minori) emesse in larga parte dal riscaldamento delle abitazioni. Queste particelle vengono infatti ritenute le principali responsabili in quanto si depositano nei polmoni, aumentando il rischio di malattie cardiovascolari e respiratorie e rendendo gli individui più vulnerabili al virus. ^[5]

Tra gli studi presi in considerazione ai fini di questa rassegna, undici includono variabili relative all’inquinamento e solo uno, Knittel et al., non riscontra una correlazione con la severità della pandemia. Occorre però considerare che l’inserimento di variabili che descrivono la qualità dell’aria presenta diverse criticità legate soprattutto alla presenza di variabili “confounding” (ovvero variabili correlate sia all’inquinamento sia alla diffusione della pandemia come, ad esempio, spostamenti e densità abitativa) e ad uno “spillover effect” dovuto alla diffusione del virus tra aree (Cole et al.). Gli studi di seguito, tenendo conto di questi possibili errori, adottano diverse metodologie per testare l’esistenza di un nesso di causalità tra inquinamento e severità della pandemia. Cole et al. effettuano diversi esercizi di sensitivity e trovano che il legame positivo tra mortalità e inquinamento è persistente. Sia Ingo et al., sia Coker et al., inseriscono variabili di controllo che tengono conto dei fattori confounding. Entrambi gli studi confermano la relazione positiva col tasso di mortalità. Un’altra possibile soluzione al problema dell’endogeneità è quella di inserire variabili strumentali correlate all’inquinamento, ma non al virus (tipicamente variabili atmosferiche). Austin et Al., analizzando i dati degli Stati Uniti, seguono questo approccio e stimano che un aumento di un microgrammo della concentrazione di PM2.5 nell’aria comporta un aumento del tasso di mortalità del 3 per cento e del 2 per cento del tasso dei contagi. Esistono anche problemi di misurazione dell’inquinamento, per ovviare ai quali Becchetti et al. effettuano una distinzione tra comuni italiani situati in aree protette (parchi regionali o nazionali) e non, sotto l’ipotesi che i primi siano meno esposti all’inquinamento. Gli autori concludono che il tasso di mortalità è inferiore nei comuni “verdi”.

Alcuni studi guardano anche alla concentrazione di altre sostanze inquinanti. In particolare, Becchetti et al., Ingo et al., Perone e Zhu et al. mostrano un legame anche con la concentrazione di PM10, di diossido di azoto e di azoto.^[6]

• Misure adottate e risposta da parte dei cittadini

Valutare l’impatto di misure restrittive si scontra con significativi problemi di endogeneità, che solo un lavoro, con una procedura in parte discutibile, prova ad affrontare, concludendo che le misure restrittive sono state efficaci nel contenimento dei decessi. Quanto ai movimenti delle persone non vi sono evidenze omogenee circa il loro ruolo nel determinare il diverso impatto della pandemia tra paesi.

Con il dilagarsi della pandemia, i diversi governi hanno adottato misure di contenimento del virus che consistono principalmente in chiusura di scuole, esercizi commerciali e confini e limitazioni negli spostamenti. Al fine di cogliere la tempestività della risposta governativa, Wu et al. includono la durata delle chiusure e trovano che la variabile è positivamente associata al tasso di mortalità. Per valutare, invece, l’intensità della risposta governativa lo studio di Sorci et al. include lo Stringency Index, ovvero un indicatore sintetico che attribuisce un punteggio ai paesi sulla base di una valutazione qualitativa dell’efficacia delle misure adottate.^[7] Gli autori trovano un legame positivo tra lo Stringency Index e il tasso di fatalità (più restrizioni, più decessi). Sia nel caso di Sorci et al., sia nel caso di Wu et al., i risultati potrebbero essere la conseguenza del fatto che paesi maggiormente colpiti hanno tendenzialmente adottato misure più stringenti. Chaudry et al. inseriscono la severità del lockdown misurata attraverso una variabile categorica (cioè una variabile che può assumere solo certi valori) e la tempestività nella chiusura dei confini e concludono che le due variabili non sono associate alla mortalità, ma risultano correlate a minori tassi di ricoveri e di contagi. Ad ogni modo, i tre studi menzionati non affrontano il problema dell’endogeneità delle variabili. Una soluzione viene suggerita da Becchetti et al. che costruiscono un trend controfattuale basato sulla tendenza dei decessi prima che misure restrittive fossero introdotte. Da questa procedura emerge che il lockdown è una misura efficace nel contenimento della pandemia. Questa metodologia dipende in modo cruciale dalla bontà della stima delle tendenze pre-lockdown. In ogni caso, essa non è replicabile all’interno del modello che presenteremo di seguito che guarda all’intero 2020 (periodo in cui le misure sono state implementate ed interrotte a più riprese).

Alcuni modelli però includono variabili relative agli spostamenti o all’utilizzo dei mezzi di trasporto. Becchetti et al., non riscontrano evidenza del ruolo che hanno avuto gli spostamenti (calcolati come flussi in entrata e in uscita dalle province italiane) nella diffusione del virus. Al contrario, Cartenì et al., concentrandosi sulle regioni italiane, concludono che il tempo medio trascorso sui mezzi e la frequentazione dei mezzi nelle tre settimane precedenti al giorno considerato, sono positivamente correlate al diffondersi della pandemia. Knittel et al. trovano una correlazione positiva tra l’uso del trasporto pubblico e la mortalità.

• Capacità dei sistemi sanitari

Non tutti i lavori introducono variabili relative alla capacità dei sistemi sanitari e, tra quelli che lo fanno i risultati sono misti. La disponibilità di risorse umane (medici e infermieri) e di letti sembra aver avuto un ruolo nel ridurre la fatalità del virus (cioè il rapporto tra decessi e contagiati), ma non la mortalità (decessi per popolazione). Alcuni lavori trovano addirittura una relazione positiva tra spesa sanitaria e fatalità del virus.

Sorprendentemente, nessun lavoro trova un legame negativo tra spesa sanitaria prima della pandemia e tasso di fatalità del virus. Al contrario, tre studi (Perone, Sorci et al. e Khan et al.) riscontrano un legame positivo. Di fronte a questo risultato contro intuitivo, questi lavori o sostengono la necessità di ulteriori ricerche in proposito o notano la possibile relazione tra livello del reddito, spesa sanitaria, età media della popolazione, e numero dei decessi. Paesi ad alto reddito hanno tipicamente un livello di spesa sanitaria elevata e una maggiore anzianità della popolazione, con quest’ultimo fattore che li espone a una più elevata mortalità. Un’altra possibile spiegazione potrebbe risiedere nella maggiore capacità di tracciamento dei decessi nei paesi con maggiore spesa sanitaria (Khan et al.).

Risultati più intuitivi riguardano invece alcuni aspetti sella spesa sanitaria:

• Riguardo il personale, Chaudry et al. riscontra una correlazione negativa tra numero di infermieri e mortalità, ma non riscontrano alcuna relazione con il numero di medici. Perone, invece, riscontra una correlazione negativa tra numero di medici e fatalità del virus.
• Riguardo i posti letto, Sorci et al. trovano una relazione negativa tra numero di posti letto e fatalità del virus. Knittel et al. e Coker et al. non trovano una relazione significativa, mentre Wu et al. trovano invece, una relazione positiva rispetto alla mortalità.
• Due studi si concentrano invece sul tasso di saturazione dei posti letto, trovando una correlazione positiva con la mortalità (Olivieri et al. e Perone). Tuttavia, questa correlazione potrebbe riflettere un legame di causalità inversa tra il tasso di saturazione dei posti letto (che causa contatti ravvicinati tra malati) e la severità della pandemia.

Oltre alla disponibilità delle risorse, bisognerebbe considerare l’efficienza del loro impiego. A tal proposito, Perone, concentrandosi sulla situazione italiana, include un indicatore di performance del sistema sanitario regionale che tiene conto di fattori quali la soddisfazione dei pazienti, l’aspettativa di vita, l’uguaglianza nel trattamento, i risultati operativi, e conclude che questa variabile ha contribuito a determinare il diverso tasso di fatalità tra regioni. Anche i risultati in Olivieri et al. comportano che dove i sistemi sanitari hanno saputo reagire prontamente, la mortalità è stata contenuta. Seguendo un approccio di clustering, gli autori suddividono le regioni in gruppi sulla base dell’incidenza dei contagi, il tasso di occupazione dei posti in terapia intensiva e la mortalità del virus. Lombardia e Veneto, pur essendo state colpite entrambe per prime e pur essendo geograficamente vicine, vengono classificate in gruppi diversi. Gli autori giustificano questo risultato col fatto che il Veneto è riuscito a contenere meglio la pandemia grazie ad un lockdown immediato e alla capacità di approvvigionarsi di strumenti sanitari, di distribuire in maniera capillare sul territorio servizi di igiene e prevenzione e di diffondere test per i sintomatici e la popolazione a rischio.

La metodologia

L’analisi presentata nel seguito introduce diverse novità rispetto agli studi presentati. La prima riguarda la scelta di un campione ristretto che comprende unicamente i paesi OCSE ad alto reddito. La scelta di includere unicamente paesi ad alto reddito ci consente di disporre di dati probabilmente più accurati relativi a paesi con caratteristiche simili. Si tratta anche dei paesi più colpiti dalla pandemia, con cui è più facile effettuare un confronto rispetto all’Italia. Il secondo tratto distintivo dell’analisi è la separazione iniziale tra le osservazioni che riguardano la popolazione più anziana e quella meno anziana per tenere conto della possibile diversità dell’effetto di diverse variabili esplicative tra le due categorie di popolazione. Terzo, prendiamo in considerazione i dati sui decessi annuali per l’intero 2020. La scelta di un arco temporale più ampio ci permette di ovviare a problemi legati alla stagionalità delle fluttuazioni dei decessi, stagionalità che è diversa a seconda della localizzazione dei paesi (si pensi solo alle differenze tra quelli dell’emisfero australe e di quello boreale). Per valutare le differenze, questa nota guarda al numero dei decessi per paese, nell’ipotesi che errori di misurazione su questa variabile siano meno forti che per altre variabili, come il numero dei contagi (che dipende da quanti tamponi sono stati fatti).

1. Campione

Il campione comprende 31 dei paesi OCSE che rientrano nella categoria di paesi “avanzati” anche secondo la classificazione del Fondo Monetario Internazionale.^[8] Dal campione dei 37 paesi OCSE, sono state quindi escluse Colombia, Cile, Messico, Polonia, Ungheria e Turchia. La decisione di includere solo i paesi ad alto reddito deriva dall’esigenza di utilizzare dati più affidabili e dall’evidenza che l’effetto delle variabili esplicative sulla mortalità non sembra essere uguale per tutti i gruppi di paesi. Tra l’altro, anche l’effetto della demografia sulla pandemia sembra essere molto diverso tra paesi avanzati ed altri paesi: secondo uno studio della World Bank il tasso di mortalità per la fascia di età 70-79 anni è 12,6 volte quello della fascia 50-59 nei paesi ad alto reddito.^[9] Nei paesi a basso reddito, invece, lo stesso rapporto è pari a 3,6. Si sarebbe potuto cercare di modellare tali differenze, ma, per semplicità e anche alla luce della minore affidabilità dei dati nei paesi non avanzati, si è preferito procedere all’analisi dei soli paesi avanzati.

2. Le variabili

L’analisi si focalizza sul numero di decessi nei vari paesi. Il motivo è che riteniamo che il margine di errore sulla misurazione di tale variabile sia inferiore a quello sul numero dei contagi.^[10] In particolare, come variabile dipendente del nostro modello abbiamo utilizzato, per ogni paese, il numero medio giornaliero dei decessi calcolato come rapporto tra il numero dei decessi totali nel 2020 diviso per il numero dei giorni in cui il paese è stato esposto alla pandemia (la sua “durata”).^[11] Focalizzarci sulla mortalità giornaliera è giustificato dal fatto che, presumibilmente il numero totale nell’anno dei decessi è più elevato nei paesi che sono stati esposti più a lungo alla pandemia. 

In linea con la letteratura passata in rassegna, le variabili indipendenti incluse nel modello tengono conto degli aspetti relativi allo stato di salute della popolazione, aspetti socioeconomici, aspetti ambientali e relativi alla capacità dei sistemi sanitari (Tav.1).

In particolare, per tenere conto dello stato di salute della popolazione e dell’aspetto socioeconomico, è stato inserito l’Indice di Sviluppo Umano (ISU), ovvero un indice che rappresenta la sintesi di tre dimensioni: salute, istruzione e ricchezza della popolazione. L’indice viene calcolato come media geometrica della speranza di vita alla nascita, degli anni di scolarizzazione per gli adulti (per la popolazione al di sotto dei 25 anni si considerano gli anni di scolarizzazione previsti) e il logaritmo del reddito nazionale lordo pro capite. Il valore fornito dalle Nazioni Unite è aggiornato al 2019.^[12]

Come variabile ambientale, è stato incluso l’inquinamento, misurato come la quota di popolazione esposta ad una concentrazione di PM2.5 che eccede le raccomandazioni dell’OMS, ovvero una soglia media annua maggiore di 10 microgrammi per metro cubo. La concentrazione dell’inquinamento è molto sensibile alle condizioni locali (monitoraggi in luoghi diversi della stessa città possono riportare concentrazioni diverse), inoltre i sistemi di misurazione possono differire tra paesi. La variabile va dunque intesa come una generica indicazione della qualità dell’aria. Il dato fornito dalla WorldBank è aggiornato al 2017.^[13]

Relativamente alla capacità sanitaria, è stata utilizzata la spesa pubblica pro capite destinata alla sanità (spesa sanitaria) nel 2018 espressa tenendo conto della parità di potere di acquisto tra paesi.^[14]

Per tenere conto di fattori che possono incrementare le occasioni di contagio, abbiamo incluso:

• Popolazione rurale: rappresenta la quota di popolazione che vive nelle zone rurali così come definite dalle statistiche nazionali (non vi è uno standard universale per la distinzione tra area urbana e area rurale). La variabile viene calcolata come la differenza tra la popolazione totale e la popolazione urbana rapportata alla popolazione totale ed è aggiornata al 2018;^[15]
• Densità abitativa: rappresenta il numero di residenti di un paese per chilometro quadrato. Il valore è aggiornato al 2018.^[16]

Abbiamo inoltre tenuto conto della dinamica temporale con cui si è manifestato il virus inserendo un “effetto sorpresa”. Come sostiene ISS (2021), i picchi di mortalità registrati durante la seconda ondata in Italia sono stati inferiori rispetto a quelli raggiunti durante la prima (il tasso di mortalità a febbraio marzo era di 26,1 decessi per 100.000 abitanti, mentre ad ottobre di 14,7). Queste differenze sono riconducibili ad un aumento della disponibilità dei servizi ospedalieri, ad un miglioramento delle conoscenze e ad un aumento della capacità diagnostica. In sostanza, l’esperienza maturata ha consentito di migliorare nel tempo la capacità di reazione alla pandemia. Allo stesso modo, è ragionevole immaginare che paesi che sono stati colpiti dopo dalla pandemia abbiano beneficiato dell’esperienza di altri paesi colpiti prima. La variabile inserita nel nostro modello relativa all’“effetto sorpresa” è calcolata come il giorno dell’anno (contato a partire dal primo gennaio) in cui il paese ha superato la soglia dei 100 casi cumulati di contagi: minore è il valore assunto dalla variabile, maggiore sarà l’effetto sorpresa.

Infine, per tenere conto del diverso impatto che la pandemia ha avuto sui paesi asiatici, caratterizzati da culture in cui i contatti fisici sono meno diffusi e in cui l’uso di strumenti di protezione quali le mascherine sono comuni, è stata inclusa una variabile dicotomica (Asia) che assume valore 1 per i paesi asiatici e 0 per gli altri.^[17]

Inizialmente sono state incluse nel modello anche altre variabili, quali il numero di visitatori dall’estero in rapporto alla popolazione, l’insularità dei vari paesi (ossia se sono isole o meno) e il numero di letti di ospedale per 100.000 abitanti, ma non sono risultate significative. Per semplicità, non si riportano le regressioni inclusive di queste variabili.

Non sono state invece incluse variabili relative alle restrizioni introdotte in risposta alla pandemia per due principali motivi. Il primo è la difficoltà di trovare buoni indicatori. L’indicatore più utilizzato, lo Stringency Index, è comunque in buona parte basato su valutazioni di tipo qualitativo. Il secondo è l’endogeneità delle restrizioni e la difficoltà di trovare adeguate variabili strumentali per ovviare al problema.^[18] Nella misura in cui la risposta alla pandemia in termini di restrizioni può essere considerata simile in tutti i paesi e influenzata prevalentemente dall’intensità della pandemia stessa, i risultati possono essere interpretati come relativi a una forma ridotta di un modello più complesso in cui la risposta della pandemia sia considerata prevalentemente endogena. Ciò non significa che i paesi abbiano avuto le stesse restrizioni, ma che differenze tra le restrizioni siano dovute a fattori non sistematici, ma casuali (che contribuirebbero al termine di errore del modello). Se invece le restrizioni fossero sistematicamente correlate, in particolare, alle variabili incluse nelle regressioni, l’omissione di una misura delle restrizioni causerebbe una distorsione nelle stime dei coefficienti delle variabili correlate di cui si dovrà tenere conto (vedi sotto). 

Tav. 1: Descrizione delle variabili
Variabili	Media	Mediana	Dev. St.
ISU	0,92	0,92	0,03
Inquinamento	56,22	68,78	40,59
Spesa sanitaria	2.632,60	2.754,69	1.034,41
Popolazione Rurale	21,21	18,57	11,55
Densità abitativa	138,12	105,05	142,10
Effetto sorpresa	69,32	71,00	8,20
Fonte: elaborazione Osservatorio CPI su dati WorldBank, John Hopkins University, World Health Organization, Nazioni Unite, WorldBank

3. Il modello

Come si è detto, una caratteristica del nostro approccio è di ipotizzare che le variabili esogene incluse nel modello potrebbero avere diversi effetti sulle diverse fasce di età della popolazione (generalmente i più anziani sono maggiormente sensibili a piccole variazioni delle variabili indipendenti come evidenziano Ingo et al.). Pertanto, sono state stimate inizialmente due diverse regressioni corrispondenti a due diverse fasce di età.

La prima è relativa ai decessi degli “anziani” (D_anziani), definiti come le persone di età superiore ai 60 o 65 anni, a seconda della suddivisione per fascia di età per cui è disponibile il dato per i vari paesi.^[19] I decessi sono stati poi divisi per la durata della pandemia espressa in giorni, come sopra definita (Durata)  per ottenere i decessi medi giornalieri. I decessi medi giornalieri sono stati espressi come funzione esponenziale delle variabili esplicative, moltiplicata per il numero di anziani (N_anziani):

 

dove X rappresenta la matrice delle variabili indipendenti, β il vettore dei coefficienti, α la costante e ε i residui. La forma esponenziale è stata adottata per tenere conto della possibilità che l’effetto di variazioni della variabile dipendente sia nonlineare, come suggerito dalla nonlinearità della diffusione del contagio.^[20] Dividendo i due lati dell’equazione per il numero di anziani ed esprimendo la relazione in logaritmo naturale, si ottiene la relazione:

dove DGP, la variabile dipendente della regressione, è la percentuale media (sul totale della popolazione anziana) dei decessi al giorno (decessi medi al giorno di anziani per ogni 100.000 anziani) durante il periodo di esposizione alla pandemia nel 2020. Per esempio, per una popolazione anziana di 15 milioni di abitanti, con decessi di 50.000 unità e un’esposizione per 300 giorni, il numero di decessi di anziani per 100.000 anziani sarebbe uguale a 1,11 e la variabile dipendente sarebbe il suo logaritmo naturale, ovvero 0,1054. Lo stesso modello è stato poi stimato per la popolazione sotto i 60/65 anni (i “giovani”). I coefficienti del modello sono stati stimati con OLS, come in sette degli studi considerati nella precedente rassegna.^[21]

Risultati

Al fine di selezionare le variabili più significative, è stata effettuata una specification search partendo da una regressione che include tutte le variabili ed eliminando via via le meno significative.

Seguendo questo approccio per la regressione degli anziani siamo arrivati a una specificazione in cui le uniche variabili significative nello spiegare i decessi giornalieri sono l’inquinamento con segno positivo, l’effetto sorpresa con segno negativo e la variabile “Asia” con segno negativo (Tav.2). I segni sono peraltro quelli attesi in base alla discussione precedente.

Una questione riguarda la possibile omissione di una variabile relativa al grado di restrizioni introdotte per effetto della pandemia, omissione che abbiamo giustificato con i problemi di misurazione di tali restrizioni e con la difficoltà a trovare variabili strumentali adeguate a risolvere la questione dell’endogenità delle restrizioni rispetto ai decessi. Come discusso tale omissione determinerebbe una distorsione dei coefficienti stimati per le variabili che sono correlate con l’eventuale indice di restrizione. Tra i regressori inclusi, il grado di inquinamento e la dummy Asia, non appaiono a priori dover essere correlati con il grado di restrizione. Il problema si pone, semmai, per l’effetto sorpresa. Si potrebbe, per esempio, ipotizzare che paesi colpiti prima dalla pandemia abbiano poi dovuto reagire con restrizioni maggiori. Se così fosse il bias sul coefficiente dell’effetto sorpresa sarebbe positivo.^[22] Se invece i paesi colpiti per primi dalla pandemia avessero poi introdotto minori restrizioni il bias sarebbe negativo.

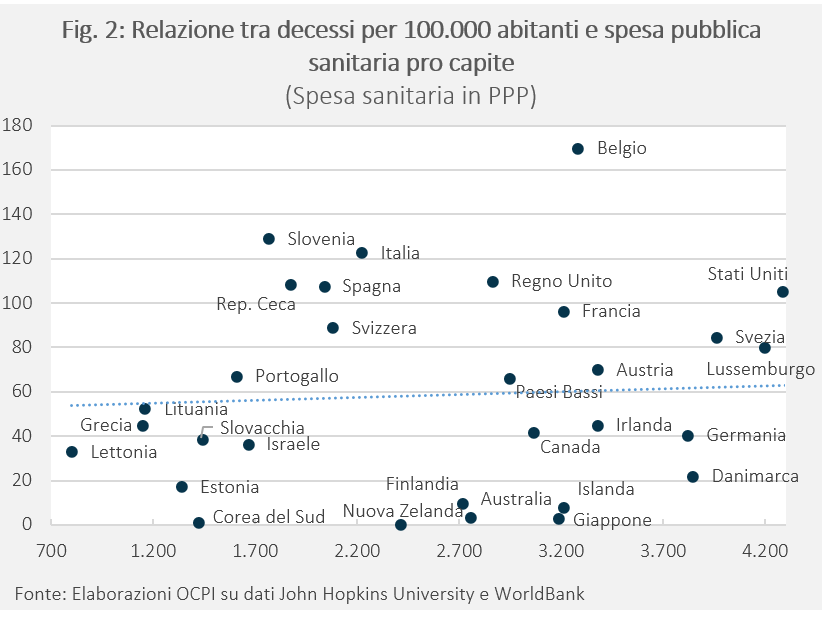
Tra le variabili non significative, invece, c’è la spesa pubblica in sanità. In effetti, paesi come Lettonia, Grecia, Lituania, Estonia, pur avendo una spesa sanitaria pubblica pro capite bassa, hanno registrato un numero di decessi contenuto. Per contro, Stati Uniti, Belgio, Francia e Regno Unito con un’alta spesa sanitaria hanno registrato un elevato numero di decessi. In generale, la relazione bivariata tra numero dei decessi e spesa sanitaria appare irrilevante (Fig.2). Come notato nella rassegna della letteratura nessun lavoro trova una relazione negativa tra spesa sanitaria e numero dei decessi. Gli unici tre lavori che trovano una relazione (Perone, Sorci et al. e Khan et al.) trovano addirittura un legame positivo, probabilmente perché (per Sorci et al. e Khan et al.) non viene fatta distinzione tra paesi avanzati e non (i paesi avanzati, che hanno spesa sanitaria più elevata, sono stati più colpiti dalla pandemia). L’assenza di un’efficacia nella spesa sanitaria passata nel proteggere dal Covid suggerisce che tale spesa non fosse mirata a ridurre gli effetti di una possibile pandemia, che in effetti ha colto tutti di sorpresa. I paesi avanzati, forse a differenza dei paesi meno sviluppati, negli anni scorsi, non avrebbero investito risorse nei settori sanitari che potevano offrire un vantaggio nella lotta contro le malattie infettive, destinando invece più risorse al contrasto di malattie più comuni (tumori, malattie cardiocircolatorie, diabete).

 

Tav. 2: Risultati del modello per la popolazione anziana (t-stat tra parentesi)
Variabili	Regressione 1	Regressione 2	Regressione 3
Costante	14,4391	10,2898	3,6624**
	(1,53)	(1,14)	(1,89)
Effetto sorpresa	-0,0639*	-0,0850***	-0,0706**
	(-2,00)	(-2,88)	(-2,63)
Inquinamento	0,0079	0,0108**	0,0135***
	(1,26)	(2,16)	(3,02)
Asia	-5,1248***	-5,0364***	-4,9503***
	(-5,15)	(-5,51)	(-5,57)
Popolazione Rurale	0,0195	0,0125
	(1,05)	(0,69)
ISU	-13,4934	-6,2535
	(-1,37)	(-0,73)
Spesa sanitaria	0,0003
	(1,10)
Densità	0,0023
	(1,13)
R2	0,644	0,603	0,575
*** Significativo al 99%, ** significativo al 95%, * significativo al 90%. Fonte: elaborazione Osservatorio CPI su dati WorldBank, John Hopkins University, World Health Organization.

Abbiamo ristimato la regressione 3 anche per la popolazione giovane, ottenendo risultati moto simili, in termini di dimensione e significatività dei coefficienti stimati, a quelli della popolazione anziana, tranne per la costante che è, come atteso vista la mortalità decisamente inferiore, molto più bassa (Tav.3).

Tav. 3: Risultati del modello per la popolazione giovane (t-stat tra parentesi)
Variabili	Coefficienti
Costante	-1,6501
	(-0,71)
Effetto sorpresa	-0,0548**
	(-1,71)
Inquinamento	0,0162***
	(3,06)
Asia	-4,4574***
	(-4,22)
R2	0,474
*** Significativo al 99%, ** significativo al 95%, * significativo al 90%. Fonte: elaborazione Osservatorio CPI su dati WorldBank, John Hopkins University, World Health Organization.

 

Tav.4: Risultati F test
Coefficienti	F-stat
Effetto sorpresa	0,13
Inquinamento	0,15
Asia	0,30
Costante	3,16
Fonte: elaborazioni OCPI

È possibile verificare attraverso un F test che i coefficienti della regressione 3 di Tav.2 e della regressione di Tav.3 non sono statisticamente diversi (Tav.4). L’unico coefficiente che diverge è la costante.

Il passo successivo è stato quindi quello di vincolare i coefficienti di tutte le variabili tra giovani ed anziani, tranne quelli relativi alla costante (Tav.5), o, cosa equivalente si è inserita una variabile dummy che assume valore 1 per le osservazioni riferite agli anziani e 0 altrimenti.

Tav. 5: Risultati del modello unico (t-stat tra parentesi)
Variabili	Coefficienti
Costante	-1,0099
	(-0,68)
Dummy anziani	4,0320***
	(15,08)
Effetto sorpresa	-0,0627***
	(-3,07)
Inquinamento	0,0148***
	(4,39)
Asia	-4,7039***
	(-6,98)
R^2	0,8351
*** Significativo al 99%, ** significativo al 95%, * significativo al 90%.

Il segno e, approssimativamente, la dimensione e la significatività dei coefficienti relativi all’effetto sorpresa, all’inquinamento e alla variabile Asia rimangono invariati. Il coefficiente positivo della dummy indica che, indipendentemente dagli altri fattori, la mortalità del virus è maggiore per la popolazione anziana.

I residui della regressione, che passano un test di normalità, danno utili indicazioni sui paesi che hanno registrato decessi particolarmente alti o bassi (Fig.3).^[23] Valori particolarmente alti (più decessi del previsto rispetto ai decessi effettivi in rapporto ai decessi effettivi) sono stati osservati per Stati Uniti, Irlanda e Svezia. Per Nuova Zelanda, Australia e Germania invece si osservano valori particolarmente bassi. Anche l’Italia ha avuto un numero di decessi basso rispetto alle previsioni del modello. Queste differenze potrebbero riflettere in parte i diversi approcci seguiti nella risposta alla pandemia (che, come si è detto, non sono stati esplicitamente inclusi nel modello) con alcuni paesi, come l’Italia, che hanno proceduto a chiusure massicce prima di altri che (come Stati Uniti, Svezia e Regno Unito) hanno tardato nell’applicazione delle misure o, addirittura, hanno inizialmente negato la rilevanza del problema.

^[24]

Cosa ci dice il modello sull’impatto delle variabili esplicative sui decessi?

Si consideri un paese con caratteristiche intermedie come la Danimarca che presenta un effetto sorpresa di 70 (a fronte di una media campionaria di 69,32), un livello di inquinamento pari al 56,91 per cento (a fronte di un inquinamento medio del 56,22 per cento) e una quota di anziani del 25,06 per cento della popolazione totale (a fronte di una media del 23,7 per cento). Per un tale paese, il modello implica che:

• un aumento dell’1 per cento della quota di popolazione esposta ad una soglia di inquinamento superiore allo standard indicato dall’OMS, comporta un aumento dei decessi dell’1,6 per cento.
• un anticipo di 1 giorno nell’effetto sorpresa comporta un aumento dei decessi del 6 per cento. Questo effetto sembra particolarmente forte ma occorre considerare che nella prima fase della pandemia il virus colse impreparate le strutture mediche e la mortalità fu particolarmente alta, rispetto ai contagi, nei paesi colpiti per primi. Per esempio, in Italia, tra i primi paesi colpiti, la metà dei decessi annuali si verificò nella prima fase (entro maggio), mentre un paese come il Portogallo, che appare con un ritardo di circa due settimane nella variabile sorpresa e con un numero di decessi complessivamente pari alla metà di quello italiano, solo il 20 per cento dei decessi si è verificato entro maggio. In altri termini, i paesi colpiti prima hanno accumulato un pesante divario in termini di decessi proprio nella prima fase della crisi.
• Aumentando dell’1 per cento la quota della popolazione anziana, i decessi stimati aumentano dello 0,5 per cento.

 

Fonti

Austin, Wes and Carattini, Stefano and Mahecha, John Gomez and Pesko, Michael, “COVID-19 Mortality and Contemporaneous Air Pollution” (2020). CESifo Working Paper No. 8609, Available at SSRN: https://ssrn.com/abstract=3711885

Becchetti, L., Conzo, G., Conzo, P., Salustri, F., 2020c. “Understanding the heterogeneity of adverse COVID-19 outcomes: the role of poor quality of air and lockdown decisions”. Doi: https://doi.org/10.2139/ssrn.3572548.

Becchetti, L., Conzo, G., Conzo, P., Salustri, F., 2020d. “Park municipalities and mortality during the COVID-19 pandemic”. Doi: https://doi.org/10.2139/ssr n.3625606.

Cartenì, A., Di Francesco, L., Martino, M., 2020. “How mobility habits influenced the spread of the COVID-19 pandemic: results from the Italian case study.” Sci. Total Environ. 741, 140489. Doi: https://doi.org/10.1016/j.scitotenv.2020.140489

Chaudhry R., George Dranitsaris, Talha Mubashir, Justyna Bartoszko, Sheila Riazi, “A country level analysis measuring the impact of government actions, country preparedness and socioeconomic factors on COVID-19 mortality and related health outcomes”, EClinicalMedicine, Volume 25, 2020, 100464, ISSN 2589-5370, Doi: https://doi.org/10.1016/j.eclinm.2020.100464.

Coker, E.S., Cavalli, L., Fabrizi, E., Guastella, G., Lippo, E., Parisi, M.L., Vergalli, S., 2020. “The effects of air pollution on COVID-19 related mortality in northern Italy”. Environ. Resour. Econ. 76 (4), 611–634. Doi: https://doi.org/10.1007/s10640-020-00486-1

Cole, M., Ozgen, C., Strobl, E., 2020. “Air Pollution Exposure and COVID-19 in Dutch Municipalities”. IZA Discussion Paper No. 13367. Doi: https://doi.org/10.1007/s10640-020-00491-4

Comunian S, Dongo D, Milani C, Palestini P. “Air Pollution and Covid-19: The Role of Particulate Matter in the Spread and Increase of Covid-19's Morbidity and Mortality”. Int J Environ Res Public Health. 2020;17(12):4487. Published 2020 Jun 22. doi: 10.3390/ijerph17124487

M. Fabiani, G. Onder, S. Boros, M. Spuri, G. Minelli, A. Mateo Urdiales, X. Andrianou, F. Riccardo, M. Del Manso, D. Petrone, L. Palmieri, M. F. Vescio, A. Bella, P. Pezzotti, Rapporto ISS COVID-19 n. 1/2021 – “Il case fatality rate dell’infezione SARS-CoV-2 a livello regionale e attraverso le differenti fasi dell’epidemia in Italia.” Versione del 20 gennaio 2021.

Khan JR, Awan N, Islam MM and Muurlink O (2020) “Healthcare Capacity, Health Expenditure, and Civil Society as Predictors of COVID-19 Case Fatalities: A Global Analysis”. Front. Public Health 8:347. Doi: https://doi.org/10.3389/fpubh.2020.00347

Knittel, C. R., B. Ozaltun (2020), "What Does and Does Not Correlate with COVID-19 Death Rates", NBER Working Paper #27391, released on June 22. Doi: https://doi.org/10.1101/2020.06.09.20126805

Olivieri, G. Palù, G. Sebastiani, “COVID-19 cumulative incidence, intensive care, and mortality in Italian regions compared to selected European countries”, International Journal of Infectious Diseases, Volume 102, 2021, Pages 363-368, ISSN 1201-9712. Doi: https://doi.org/10.1016/j.ijid.2020.10.070

G.   Landoni, N.   Maimeri, M.   Fedrizzi, S.   Fresilli, A.  Kuzovlev, V.   Likhvantsev, P.  Nardelli, A.  Zangrillo, “Why are Asian countries outperforming the Western world in controlling COVID-19 pandemic?”, Pathogens and Global Health, Volume 115, n.1, pages 70-72, 2021, Doi: https://doi.org/10.1080/20477724.2020.1850982

Leuzzi L., Marinari E., Parisi G., Ricci-Tersenghi F., 2020. “La letalità apparente e quella reale di COVID-19”, https://www.lescienze.it/news/2020/05/13/news/covid-19_differenza_andamento_curve_letalita_apparente_reale-4726700/

Perone, G., 2020. “The determinants of COVID-19 case fatality rate (CFR) in the Italian regions and provinces: an analysis of environmental, demographic, and healthcare factors”. Sci. Total Environ. 142523. Doi: https://doi.org/10.1016/j.scitotenv.2020.142523

Shapiro, S. S., and M. B. Wilk. “An Analysis of Variance Test for Normality (Complete Samples).” Biometrika, vol. 52, no. 3/4, 1965, pp. 591–611. JSTOR. https://doi.org/10.2307/2333709

Sorci, G., Faivre, B. & Morand, S. “Explaining among-country variation in COVID-19 case fatality rate”. Sci Rep 10, 18909 (2020). Doi: https://doi.org/10.1038/s41598-020-75848-2

Sphording, Ingo E., Pestel, Nico, 2020. “Pandemic Meets Pollution: Poor Air Quality Increases Deaths by COVID-19”. IZA Discussion Paper No. 13418.

Stevens H., 17 marzo 2020, “Perché epidemie come il coronavirus si diffondono in modo esponenziale e come “appiattire la curva””, https://www.washingtonpost.com/graphics/2020/health/corona-simulation-italian/

Suvilehto JT, Nummenmaa L, Harada T, Dunbar RIM, Hari R, Turner R, Sadato N, Kitada R. 2019 “Cross-cultural similarity in relationship-specific social touching”. Proc. R. Soc. B 286: 20190467. http://dx.doi.org/10.1098/rspb.2019.0467

Wong B, (2020), “Why East Asians Were Wearing Masks Long Before COVID-19” https://www.huffpost.com/entry/east-asian-countries-face-masks-before-covid_l_5f63a43fc5b61845586837f4

Wu, X., R. C. Nethery, B. M. Sabath, D. Braun, and F. Dominici (2020): “Exposure to air pollution and COVID-19 mortality in the United States” medRxiv. Doi: https://doi.org/10.1101/2020.04.05.20054502

Zhu Y., Xie J., Huang F., Cao L. “Association between short-term exposure to air pollution and COVID-19 infection: evidence from China”. Sci.Tot. Environ. 2020;727 doi: https://doi.org/10.1016/j.scitotenv.2020.138704

Maria A. Zoran, Roxana S. Savastru, Dan M. Savastru, Marina N. Tautan, “Assessing the relationship between surface levels of PM2.5 and PM10 particulate matter impact on COVID-19 in Milan, Italy”, Science of The Total Environment, Volume 738, 2020, 139825, ISSN 0048-9697, https://doi.org/10.1016/j.scitotenv.2020.139825.

Sitografia

https://covid19.min-saude.pt/wp-content/uploads/2020/08/167_DGS_boletim_20200816.pdf

https://covid19.public.lu/fr/graph.html

https://covid19.ssi.dk/overvagningsdata/download-fil-med-overvaagningdata

https://covid19-surveillance-report.ecdc.europa.eu/

https://data.worldbank.org/indicator

https://elpais.com/sociedad/2020-03-22/radiografia-por-edades-del-coronavirus-en-espana.html

https://eody.gov.gr/wp-content/uploads/2021/01/covid-gr-daily-report-20210103.pdf

https://experience.arcgis.com/experience/92e9bb33fac744c9a084381fc35aa3c7

http://hdr.undp.org/en/data

https://health-infobase.canada.ca/src/data/covidLive/Epidemiological-summary-of-COVID-19-cases-in-Canada-Canada.ca.pdf

https://sam.lrv.lt/en/news/most-deaths-from-coronavirus-had-chronic-diseases

https://www.abs.gov.au/articles/covid-19-mortality-0#covid-19-mortality-by-age-and-sex

https://www.covid.is/data

https://www.cso.ie/en/releasesandpublications/br/b-cdc/covid-19deathsandcases/

https://www.fhi.no/en/id/infectious-diseases/coronavirus/daily-reports/daily-reports-COVID19/

https://www.health.govt.nz/our-work/diseases-and-conditions/covid-19-novel-coronavirus/covid-19-data-and-statistics/covid-19-case-demographics

https://www.heritage.org/data-visualizations/public-health/covid-19-deaths-by-age/

https://www.ined.fr/fichier/rte/39/PyrJ28%20J46_ENG2.jpg

https://www.oecd.org

https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/weeklyprovisionalfiguresondeathsregisteredinenglandandwales

https://ourworldindata.org

https://www.rivm.nl/coronavirus-covid-19/grafieken

https://www.science.co.il/medical/coronavirus/Death-statistics.php

https://www.sciencedirect.com/science/article/pii/S1201971220321949

https://www.spkc.gov.lv/lv/aktualitates-par-covid-19

https://www.statista.com